いつもいつも思っているのが
毎日、面白い業種のゲストがいらっしゃるわけです。
そんな日々を忘れたくないのでちょっと書き留めていこうと
思います。
//////////
今回は数学者。
数学など数字を扱う全般が全くダメな私にとって
鬼門でしかないその学問は
高校2年ぐらいでギブアップしてから見たくもない
ものでした。
昨日のゲストは日本語がペラペラ、エリザさん。
フランスで数学の研究をしているんだそう。
「数学者。。。あの福山雅治がやってたガリレオ的な?
なんなら容疑者Xの堤真一が数式の美しさを求めていたような
証明とかする人???」と訊いたところ
 (カッコ良かったですねー。堤さん。こんな学術肌が大好きです)
(カッコ良かったですねー。堤さん。こんな学術肌が大好きです)
私がやっているのは「optimal control 」だよ。と。
「Optimal control」……
聞いたことがないよ。。。 ( ;∀;)
翻訳したら「最適制御」
( ̄へ ̄|||)
ウーーーーーン。想像できるような、
でもあくまで想像の範囲を出ない。。。
研究内容が、そのoptimal controlなの?と聞くと
「私が毎日やっている計算はねー
Hyperbolic equationだよ!」と。
Hyperbolic equation!!!! (★゜∀゜★)ノ?
聞いたことがないよ。。。 ?
辞書で調べると「双曲形方程式」とな・。。。
わからない! ( ;∀;)
日本語でもわかんない。。。。
コトバンクでググってみました
↓ ↓
「偏微分方程式の一つ。双曲型方程式の基本的な形は, ∂2u/∂t2=c2⊿u ……(1) (⊿=∂2/∂x12+……+∂2/∂xn2) と書かれる。ここでcは正の定数である。物理的には振動や波動を記述する方程式であって,未知関数u=u(t,x)は点x=(x1,……,xn)の時刻tにおける変位を表す。通常,方程式(1)の解で初期条件,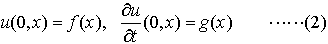 を満たすものを求めることが問題になる。これを双曲型偏微分方程式の初期値問題という。」
を満たすものを求めることが問題になる。これを双曲型偏微分方程式の初期値問題という。」
ε=ε=((((((((◎ノ・へ・)ノ もう降参です!
「エリザさん、私にゃ、
英語も日本語でも、わからんですたい・・・」
と完全降参していると
「双曲形方程式を説明。。うんとねー、
例えば、これだとわかるかも」
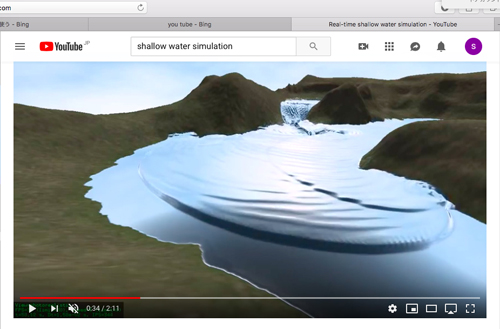
とyou tubeで説明してくれました。
この水の流れって環境によって均等にならないから..
例えば波が盛り上がるこの部分の流れについて
どんな高さ、どんな速さ、になるのか。
どんな流れになるのか、それをコンピューターに
計算させるための数式を考えるのが私たちなのよ。」
わかるような、わからないような、ですが
なんとなく、3%くらいイメージができてきました。。。
(まだまだですが)
「コンピューターって、バカなんだよ。
こういう風に計算して、っていうと計算してくれる。
それは得意。
でも想像ができないからね。
その想像をするのが人間だから」
ほうほうほう!
「数字と向き合う数学と、
絵と向き合う数学がある。
私は、絵と向き合う数学をやっているのよ」
なんと。まさかそんな言葉がくると思わなかった。
数学と、絵。
数学嫌いの私は 数字=数学=嫌い!苦手!
という単純な図式で考えていたのだけれど
確かにそうだよね。ダビンチの絵も結局は数学だし
………
なんだか面白い。
(ちなみにエッシャーの絵は数学なんだとか。
その図形の並べ方も聞きましたが、さっぱり理解不能でしたw
エリザさん、ありがとうございました!
姫路の安宿 Budget hostel for backpackers Himeji588 Guesthouse




コメント